研究紹介
蛭川研究室
教員
研究分野
数理統計学,特に時系列解析,金融工学
研究テーマ
- 非定常時系列解析の漸近理論
- 統計的漸近最適な時系列手法の金融・保険分野への応用
研究概要
時と共に変動する偶然量の観測値の系列を時系列という
数学的にはこの系列を1つの確率過程(確率変数の族)の実現したものとみなす
確率過程の統計解析を時系列解析という
通常の統計学の議論は主に独立標本に対する議論である
独立標本 $X_1,X_2,\ldots,X_n,\ldots$ $\Rightarrow$ 独立同一分布(i.i.d.)
時系列解析は過去、現在、未来の系列が
互いに従属している(影響しあっている)状況での統計解析である
$\Rightarrow$ より一般的な設定のもとでの統計解析の議論である
$X_1,X_2,\ldots,X_t,\ldots$ 従属(dependent)
$\qquad\qquad\quad\Downarrow $
確率過程 $\left\{X_t\right\}$$\Longrightarrow X_1,\ldots,X_n$ 観測系列が得られる
$\qquad\qquad\quad\uparrow$ $\qquad\qquad\swarrow $
構造についての意見を述べる
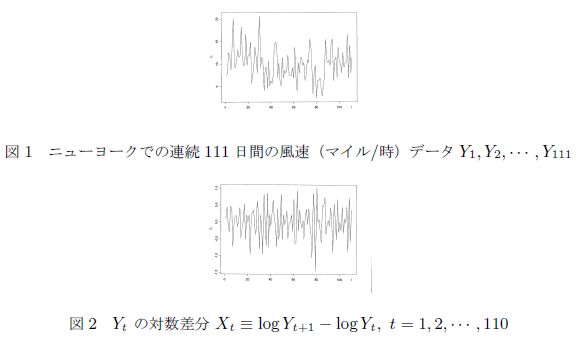
観測系列: $X_1,X_2,\cdots,X_n$ が得られたとき
標本自己相関関数 sample autocorrelation function
\begin{align*}
SACF(l) \equiv \frac{\sum_{t=1}^{n-l}(X_{t+l}-\bar X_n)(X_t-\bar X_n)}{\sum_{t=1}^n(X_t-\bar X_n)^2}
\end{align*}
の動きをみることが多い。ただし、 $\bar X_n = n^{-1} \sum_{t=1}^n X_t$
$X_{t+l}$ と $X_t$ の相関の強さを表す指標
$\left\{X_t\right\}$ が互いに独立、あるいは無相関であれば $\Rightarrow$ $SACF(l) \approx 0$ for $l \not = 0$
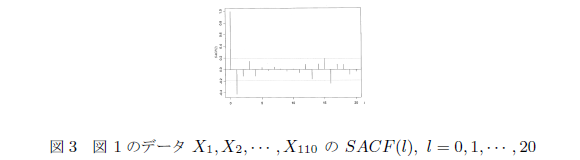
$SACF(l)$ は $l \not =0$ のときもかなり大きい値をとる $l$ がある
$\Rightarrow$ $\left\{X_t\right\}$ が互いに独立、あるいは無相関であるとは想定し難い
$\Rightarrow$ このようなデータに対してどのような時系列モデルを構成すればよいであろうか?
$\qquad \Downarrow \qquad$ 回帰分析的な考えに立てば
$X_t$ がそれ自身の過去の値 $X_{t-1},\cdots,X_{t-p}$ の線形結合と誤差項 $u_t$ の和で表されるモデル
\begin{align}\label{eq:6.2}
X_t = -b_1 X_{t-1} - \cdots -b_p X_{t-p} + u_t \tag{1}
\end{align}
を思いつくだろう。ここに、 $\{u_t\} \sim i.i.d\ (0,\sigma^2)$
$\{X_t\}$ は $p$次の自己回帰過程 $p$th order autoregressive model (AR($p$))と呼ばれる
以後、$\{X_t\} \sim \mbox{AR}(p)$ と表記する
$\Rightarrow$ 従属データへのモデルとして、最も簡単で説明力のあるモデル
上述の風速データ $X_1,X_2,\cdots,X_{110}$ が (1) 型のモデルに従っていると想定する
次数 $p$ 係数 $b_1,\cdots,b_p$ と $u_t$ の分散 $\sigma^2$ は未知だからデータから推測しなくてはならない
$\Downarrow$ (詳細を省いて結果だけ述べると)
標準的な推測法を用いて未知パラメータ $(p,b_1,\cdots,b_p,\sigma^2)$ を推定するとその推定値は
\begin{align*}
(\hat p,\hat b_1,\cdots,\hat b_p,\hat \sigma^2) =
(4, 0.6452 , 0.5079 , 0.2233 , 0.1766 , 0.1647)
\end{align*}
となり、$\{X_t\} \sim \mbox{AR}(4)$ となった。現時点の(気象現象の)値 $X_t$ が過去4時点前までの値 $X_{t-1},\cdots,X_{t-4}$ に影響を受けていることを意味している
理学を目指すあなたへ
当研究室では、(i)数理統計学 (advanced):数理統計学に関する基礎的な内容をより詳細に学ぶ(ii)時系列解析:時系列解析の基礎や最新のトピックスについて学ぶ(iii)金融工学・保険数理の統計的推測:リスク管理、ポートフォリオ管理についてのファイナンスの基礎理論や生命保険・年金・損害保険といった保険数理について学ぶ、等のテーマでセミナーを行います
