数学プログラム
Mathematics Program
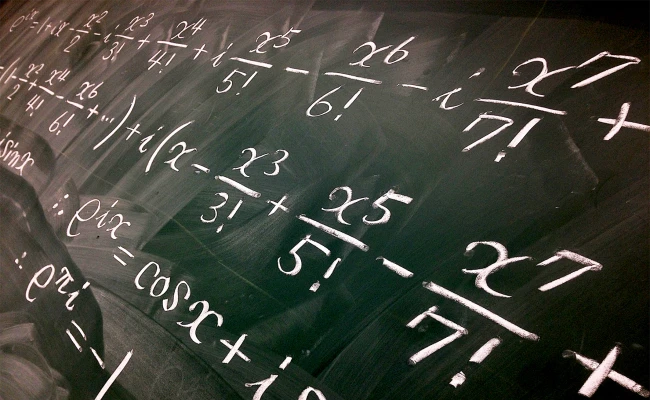

数学のすすめ
数学はあらゆる現象を記述する上で必要不可欠な「言語」です。
数学によって記述される現象を観てみませんか。
数学によって記述される現象を観てみませんか。
数学とは?
目には見えなくても、たとえばスマートフォンのように身の回りにあるものから宇宙にロケットを発射する時でさえも、数学はありとあらゆる場面に登場する学問です。数学では数や集合で成り立つ関係を調べます。

お勧めポイントは?
本数学プログラムでは、社会から求められている「数学的な考え方を用いて、問題点を整理し解決する力」を身につけることができます。

研究の特徴は?
数学には解析学、代数学、幾何学、応用数学といった様々な分野がありますが、本数学プログラムにはそれらが一通りそろっています。興味ある分野を学び、大学院へ進学し専門性を深めることも、数学と他分野にまたがる領域を学び応用力を身につけることも可能です。

教育の特徴は?
本数学プログラムでは1、2年次に数学の基礎を固め、3年次からはそれぞれの興味に応じた専門科目を解析学、代数学、幾何学、応用数学から選んで学ぶことができます。特定の分野を中心に学ぶことも、また数学の理論から応用までを幅広く学ぶことも可能です。特に理論数学だけでなく応用数学科目も充実していることが本数学プログラムの特徴です。

授業紹介
関数解析学A, B
高校では自由に関数を微分しますが、どの点でも微分できない連続関数の存在が知られています。そのような関数はたくさんあるのでしょうか?
代数系ⅡA, ⅡB
5次方程式には解の公式が存在しません。2次、3次、4次の場合には解の公式は実際につくれますが、公式が存在しないことはどうやったら証明できるのでしょうか?大学の代数系授業の1つの到達点として「ガロア理論」を学びます。
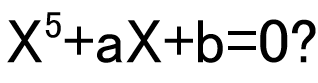
幾何学ⅡA, ⅡB
地球儀や地図帳には、座標と思える線があります。この考えを深めて、座標の導入法や微積分の応用法について学びます。可微分多様体論入門講義です。
オペレーションズ・リサーチ
たとえば「お店の商品をどこに、どのように並べれば売り上げがよくなるか」という問題を、数学を用いて解決する方法を学びます。
ほかにも魅力的な授業科目がたくさんあります!
微分積分学IA, 微分積分学IB, 線形代数IA, 線形代数IB, 数学演習A, 数学演習B, 微分積分学IIA, 微分積分学IIB, 線形代数IIA, 線形代数IIB, 解析学序論A, 解析学序論B, 代数・幾何学序論A, 代数・幾何学序論B, 集合と位相入門A, 集合と位相入門B, 数学講究
2つの学習方法(専門力プログラムと総合力プログラム)があります
専門力プログラム
専門力プログラムでは数学そのものを学び、深く理解することを目指します。卒業生は在学中に身につけた力を活かし、数学教員やシステム・ソフトウェア開発に携わるIT業界、銀行・証券・保険などの金融業界、自動車や鉄道関連企業などで幅広く活躍しています。さらに深く数学を学びたい人の多くは大学院に進学して,高度な数学を学んでいます。

総合力プログラム
数学を学ぶ上での基礎を1、2年次に固め、物理学等の他プログラム科目を並行して学ぶことにより3、4年次には数理物理学などの学際分野や応用数学の基礎知識を獲得することができます。卒業後の進路は、アクチュアリー、証券アナリスト、ファンドマネージャーやクオンツアナリストなどの金融業界への就職が考えられます。

研究の紹介


数論、代数幾何学とミレニアム賞問題
星 明考 教授
数学の中でも数論、代数幾何学とよばれる分野の研究をしています。数学にはミレニアム賞問題という2000年にアメリカのクレイ数学研究所が発表した100万ドルの賞金が懸けられた7つの重要な問題があります。そのうちの1つ「ポアンカレ予想」はロシア人数学者グリゴリー・ペレルマンによって解かれましたが、残りの6つは未解決のままです。私の研究は、この残りの6つの問題のうちの3つの問題「リーマン予想」、「ホッジ予想」、「バーチ-スウィナートン・ダイヤー予想(BSD予想)」に関係しています。数論にはこの他にも、360年という時を経て、1994年にプリンストン大学のアンドリュー・ワイルズによって解かれた「フェルマーの最終定理」や「abc予想」、「双子素数予想」などの多くの有名な未解決問題があります。
数論は、代数的整数論、解析的整数論、ゼータ関数、楕円曲線や保型形式、数論幾何学や代数幾何学など様々な分野が関連しながら発展を続けており、古くは高木貞治による類体論、岩澤健吉による岩澤理論など、これまでそして現在も日本人数学者の貢献も多い分野です。数論、代数幾何学は数学の中でも大変魅力的な研究分野として、世界中の大学・研究機関で日々研究が進められています。私もこの2つの主題が交錯する研究分野で、数学的な現象の解明を目指し、エキサイティングに日々研究を行っています。
就職状況
中学校・高等学校数学教員、公務員、システム・ソフトウェア開発、
銀行、証券、保険、自動車、鉄道、不動産、
建築などの多種多様な企業への就職実績があります。
大学院に進学し、数学をさらに深く学ぶことも可能です。
就職先の例(順不同)
㈱第四北越銀行、㈱大光銀行、福島銀行㈱、群馬銀行㈱、アクセンチュア㈱、野村証券㈱、SMBCフレンド証券㈱、丸三証券㈱、明治安田生命保険相互会社、キヤノンイメージングシステムス㈱、沖テータ㈱、㈱富士通新潟システムズ、NECソリューションイノベータ株、京セラコミュニケーションシステム㈱、㈱日立ソリューションズ東日本、越後交通㈱、㈱NSGホールディングス、東日本旅客鉄道㈱、㈱BSNアイネット、㈱原信、JA全農にいがた、警視庁警察官、国税専門官、新潟市職員、国立大学法人新潟大学
