研究紹介
應和研究室
教員
研究分野
偏微分方程式論
研究テーマ
- 保存則方程式の解の存在とその解の性質について
研究概要
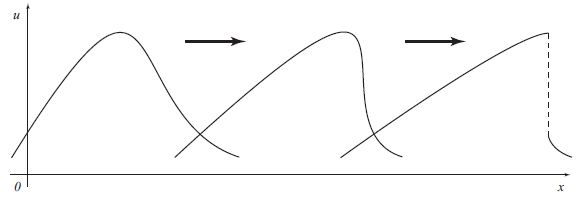
自然界に現れる波動現象の1次元的モデルである, 次の偏微分方程式を研究しています: $$ \frac{\partial }{\partial t}u(x,t)+\frac{\partial}{\partial x}f\big(u(x,t) \big)=0, \quad -\infty < x < \infty, \ t > 0. $$ ここで, $x$ は位置, $t$ は時間, $u$ は波の形を表す関数, $f$ は波を動かす力の関数です. この方程式は保存則方程式と呼ばれ, 質量保存則, 運動量保存則, エネルギー保存則などと密接に関わっています. 一般的に, $f$ という関数は自然界に現れる種々の波動現象に対応して与えられているため, 保存則方程式を満たしている $u\ $(保存則方程式の解)が存在するか(求められるか)どうかの議論は非常に大切だと言えます. しかし, 保存則方程式は, 時間変化とともに上の図のような不連続現象が現れるため, 微分可能な関数の枠組みの中で解くことができません (より詳しく知りたいという方は<http://mathweb.sc.niigata-u.ac.jp/pages/staff_research_introduce/Hiroki_Ohwa.pdf>を参照してください). そのため, 新しい解の概念を導入し, 微分可能でない関数の枠組みの中で解く必要が出てきます.
理学を目指すあなたへ
数学とは, 将来, 何に結びつくのかハッキリと見えない学問かもしれません. しかし, 数学を用いれば, 複雑な問題をシンプルに表現でき, 美しく解決することができます. このような美しさを持つ数学を学べば学ぶほど, 何か謎めいた魅力を感じ, 数学にのめりこんでいくと思います. 皆さんも, 魅力満載の数学を学んでみてはいかがでしょうか?
