鈴木研究室

教員

• 鈴木　有祐　教授

研究分野

位相幾何学的グラフ理論

研究テーマ

1. 再埋蔵に関する研究
2. 局所変形に関する研究
3. 1-交差埋め込みの研究

研究概要

　みなさんは有名な四色問題を知っていますか？ 私の研究する位相幾何学的グラフ理論において，最も有名な問題（定理）と言っても良いものだと思います．その問題は「平面上の地図は何色あれば塗り分け可能か？（隣り合う国を別の色で塗るというルールで．）」という，誰にでも理解できる非常に単純なものです．

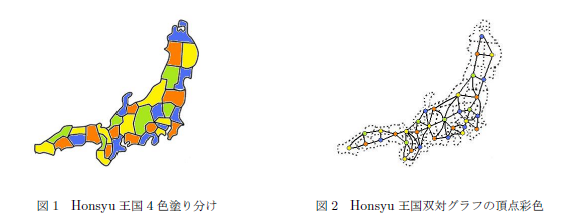
　上記の問題は，対応する領域に点（頂点）を配置し，隣接する領域どうしを線（辺）で結んでできた（離散）グラフという図形の問題と考えることができます．それらのグラフの頂点が何色で塗り分けられるのか？ 図1と図2を対応させれば，それらの問題が全く同じものであることを理解するのは難しくないでしょう．一見すると簡単そうな話ですが，この問題が提起されてから解決に至るまで実に100年以上の月日がかかっています．（1976年，K.AppelとW.Hakenにより「平面上の地図は4色あれば塗り分け可能である．」という事実が証明されています．）

　グラフ理論とは組合せ論の中の中心的な一分野で，近年のコンピュータ，ネットワーク等の発達とともに成長してきた数学です．扱うのは上述の“頂点”と“辺”からなる“グラフ”と呼ばれる図形です．実際はもう少し抽象的に，「集合$V$とその$2$元部分集合$E \subseteq {V \choose{2}}$の組$(V,E)$」と定義されます．このようにして定義されたグラフの構造を明らかにしていく,大雑把に言うとこれがグラフ理論の研究です．さらに，球面（平面）や浮き輪の表面（トーラス）のような舞台（閉曲面と呼ばれる）に辺の公差なく描画された（埋め込まれた）グラフを研究対象とするのが位相幾何学的グラフ理論です．私の研究室では，特に（閉曲面上のグラフの）再埋蔵理論，局所変形理論，1-交差埋め込み等に焦点を当て研究を行っています．

理学を目指すあなたへ

　「数学」＝「計算」と思っていると，大学で学ぶ数学の理解には程遠いかもしれません．さまざまな現象に純粋な興味を持ち，時間をじっくりかけて考えようという姿勢の身についている人が大学の数学を学ぶのに向いていると思います．