研究紹介
折田研究室
教員
研究分野
位相幾何学(特に,微分位相幾何学,シンプレクティック幾何学)
研究テーマ
- ハミルトン力学系における周期軌道の存在問題
- 重い集合,超重い集合に関する研究
- モース理論,パーシステント加群の応用
研究概要
本研究室では,幾何学,特に位相幾何学(トポロジー)を研究しています。 位相幾何学は「柔らかい幾何学」としばしば呼ばれるように,図形の角度や曲率,体積等を一旦気にせず,グニャグニャと変形させて互いに移り合う図形を同じと見做します。 例えば,ドーナツとコーヒーカップは,連続変形で互いに移り合うため,位相幾何学では同じ図形と見做せます。
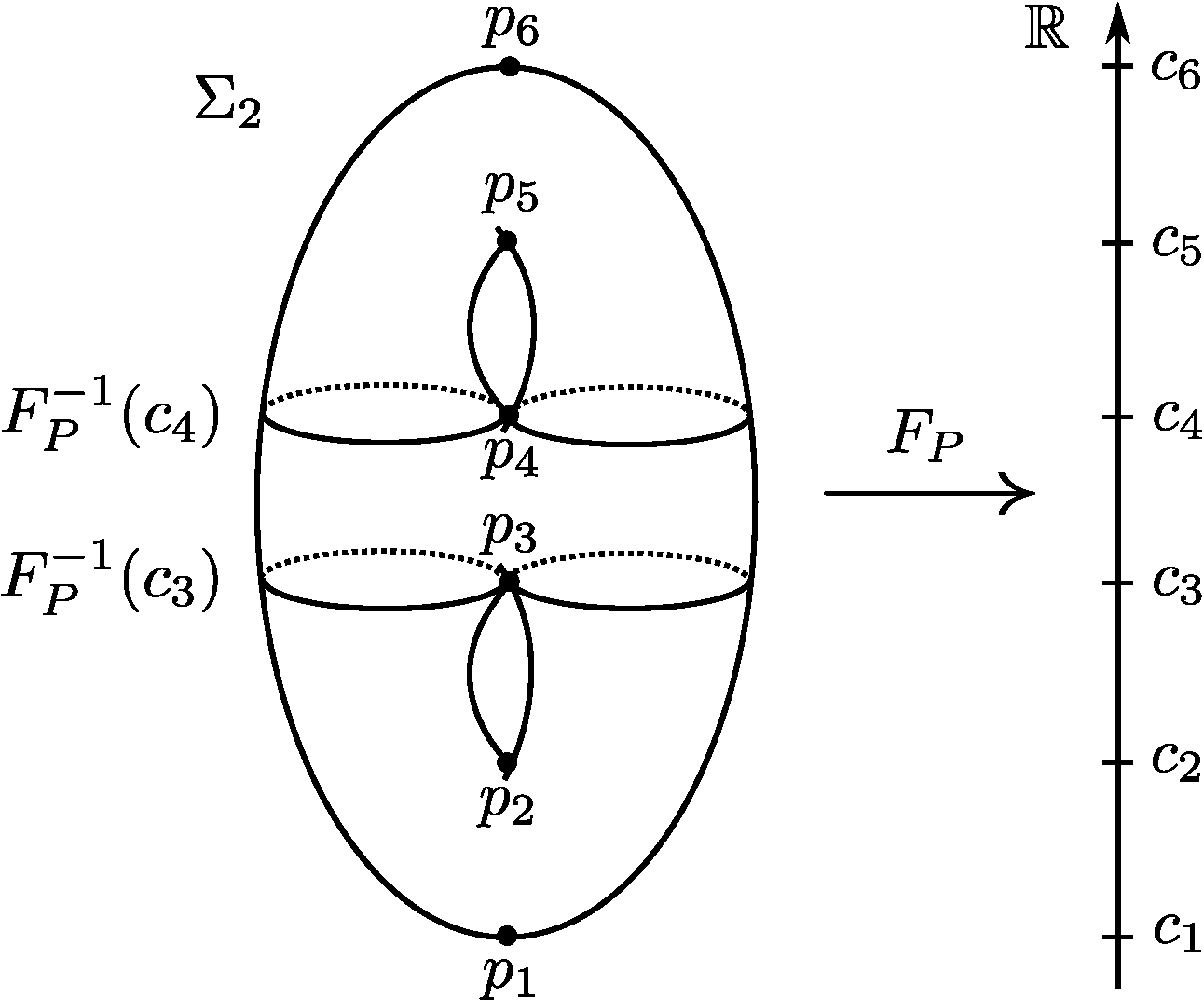
位相幾何学における重要な理論として,モース理論があります。 モース理論では,図形上の関数を考え,その微分が0になる点(臨界点)の周りを調べることにより,図形の全体像を復元することができる理論です。 ここでいう「図形」は,目に見えるものとは限らず,高次元の図形である多様体を指します。 つまりモース理論は,多様体上の関数の臨界点という局所的な情報から,多様体全体の大域的な情報を引き出す理論と言い換えられます。
数学において,関数の臨界点を調べることは非常に重要です。 高校数学では,関数のグラフの概形を描くのに用いました。 現代数学においても,微分幾何学における測地線(光の通る道が一例)は,道の空間上のエネルギー汎関数の臨界点であり, 解析力学($\rightsquigarrow$シンプレクティック幾何学,ハミルトン力学系)における物体の運動(天体の軌道などの三体問題が一例)はループ空間上の作用汎関数の臨界点となっています($\rightsquigarrow$フレアー理論)。 本研究室では,モース理論の応用を主軸に,微分位相幾何学やシンプレクティック幾何学について研究しています。
理学を目指すあなたへ
計算がメインだった高校数学までとは打って変わって,大学の数学では,現代の「理学」を支える理論を学びます。数学は論理が厳密な分,非常に自由です。勇気と楽観を持って堪能してください。
