研究紹介
田中研究室
教員
研究分野
凸解析,最適化理論,オペレーションズ・リサーチ
研究テーマ
- ベクトル値ミニマックス理論と多規準ゲームに関する研究
- 凸解析学に基づいた集合値不等式に関する研究
- ベクトル最適化,集合最適化に関する研究
研究概要
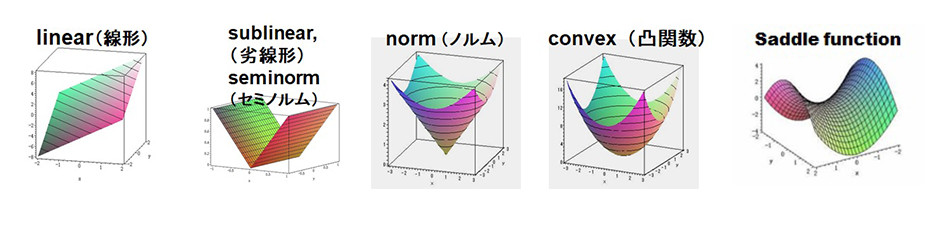
皆さんは2次関数を知っていますか? たぶん,$y=x^{2}$などの一変数なら中学校でも習うと思います。 高等学校の数学では,その関数のグラフの接線を考えたりします。 その接線を動かしてみると元のグラフがちょうど包絡線になっていることに気が付きませんか? 二変数ならどうでしょう?関数$f(x,y)=x^{2}+y^{2}$のグラフ$z=f(x,y)$を想像して見て下さい。 上の図の中に答えがあります。そうです,二人で両手で持っているシーツ(袋)の ような形をしています。丁度,切り口($y=0$の時)が$z=x^{2}$のグラフになっています。 この場合もたくさんの接平面がなす包絡線が元のグラフを表しているようです。
元々,接線や接平面は1次関数のグラフです。 実は,下に凸な2次関数(これは凸関数の簡単な例です)は一次関数の点別上限で表現できることが 一般に証明されています。それを証明するには,いくつか準備が必要で,その内容をまとめた理論が 凸解析学といいます。 凸解析学の分野では,凸集合の定義と性質,共通部分がない2つの凸集合の分離定理などを最初に学びます。その後,『凸集合は半空間の共通部分として表現でき, 凸関数はアフィン関数の点別上限関数として表現できる』などを学習します。分離定理は,Hahn–Banach separation theorem とも呼ばれ,数学的にもとても美しく,数学はもちろん,経済学やゲーム理論など多くの分野へ応用されている定理です。
「凸集合(とつしゅうごう)」とは,中身の詰まった円や正方形のようなへこみの無い形をしています。 凸解析学を端的にいうと,そのような凸集合の性質を明らかにする学問ということになります。 【「凸性」の概念は線形と非線形の橋渡し】を直感的,数学的に解明して, 数理計画などの最適化分野への応用を可能とする理論といった感じでしょうか。
私の研究室では,ベクトルや集合の比較を凸解析学を利用して行っています。 ゲーム理論やファジィ理論も出てきます。球技などのスポーツチームの比較をするには, ずば抜けたプレイヤーがいるだけでは強いチームとは言えません。皆さんならどのように, チームとチームを比較しますか?
理学を目指すあなたへ
「最適化」とは人間が数学を使って社会をよりよくする際に具現化されたものです。 そのため,最適な選択,設計,運用,決定などを効率良く行うためには,数学でものを考える スキルが必要となります。21世紀の豊かな社会は皆さんの力で実現されるものだと思います。
