研究紹介
山田研究室
教員
研究分野
オペレーションズ・リサーチ,数理計画法,大域的最適化
研究テーマ
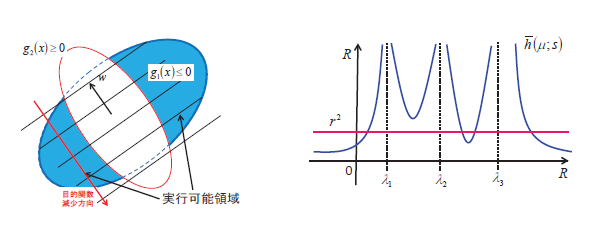
- DC計画問題に対する大域的最適化手法の開発
- 有効解集合上での最適化問題に対する逐次近似解法の開発
研究概要
企業経営や政党の意思決定において直面する多くの問題が数理モデルで表すことができます。数理モデルのなかでも,等式条件や不等式条件を満たし,ある関数の値を最小または最大にする問題は数理計画問題とよばれます。具体的には,企業におけるコスト削減問題やパソコンなどの精密機械を設計する際の配置問題などが数理計画問題で表すことができ,そのようなモデルを解くことで実社会で生じている問題に対して最善策を提案することができます。
私たちの研究室では,様々な数理計画問題の性質を調べ,最適解を求めるアルゴリズムの開発・改善を行っています。数理計画問題の解には,等式条件や不等式条件で与えられる実行可能領域上で最も良い大域的最適解の他に,実行可能領域上で最も良いとは限らないがその解の近傍上では一番良い解であることが保証されている局所的最適解があります。また,局所的最適解が必ずしも大域的最適解であるとは限らない数理計画問題は大域的最適化問題と呼ばれます。近年,数理計画問題に対する解法の研究としては,局所的最適解を求めるアルゴリズムの開発,または大域的最適解の近似解が求まることを数学的に証明することはできないが経験的・実験的に大域的最適解の近似解が求まることが保証できるヒューリスティック手法の構築が主流となっています。これに対し,私たちの研究では,アルゴリズムから生成される暫定解列が大域的最適解に収束することを数学的に証明できるアルゴリズムの構築を行っています。このようなアルゴリズムは大域的最適化アルゴリズムと呼ばれ,前述のものと比べると計算速度は遅くなりますが,精度の高い近似解が求まるという利点があります。最近の研究成果としては,数理計画問題の中でも解くのが難しいとされているDC2次計画問題に対して,従来よりも変数の数が多くても有効な大域的最適化アルゴリズムの開発に成功しています。
理学を目指すあなたへ
私たちの研究は,試行錯誤を繰り返し,失敗の連続です。しかし,失敗を繰り返すことで,最初はわからなかった関数や集合の性質が見えてきます。何事にも根気強く取り組める方をお待ちしています。
